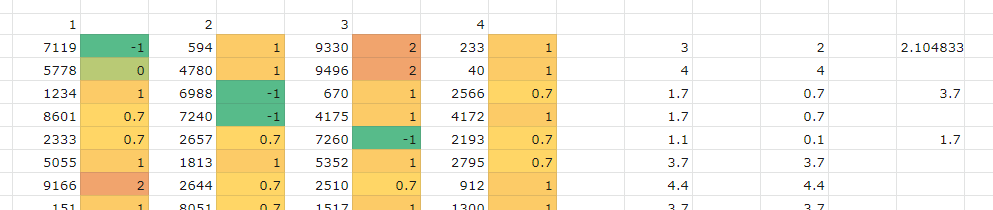
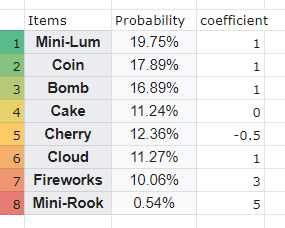
A while ago some heroes of the community approximated the chance of each Lum’s item
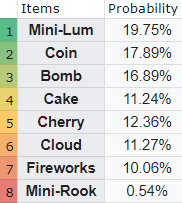
I don’t know why the numbers are so ununiform, but this is empirical data I used for my research
As you may know, when Lum does the Jackpot gS, it’s frustrating. While you can just throw it on reaction if you were not doing something but standing in throw range, it doesn’t coexist with the fact that Lum players are not idiots, and lots of matches have been lost due to chip damage on Jackpot.
Well, that isn’t guaranteed, Lum could get 4 cherries and throw them right at the opponent’s face. The question of today is what is statistically guaranteed to get from Jackpot at optimal range.
- What is optimal range?
Roughly in range of the Bomb, around range of the Coin and the Cloud is the optimal range for the case
(On picture: Suboptimal)
- What is guaranteed?
Once you, as Lum’s opponent start blocking, you can’t unblock without losing more health - How do we evaluate the damage of each item?
Arbitrary, mostly. First of all we have to consider that chip damage isn’t all born the same, first chip damage isn’t worth as much as the third chip damage, and third chip damage on 8 hp isn’t worth the same as third chip on 1 hp. But since Jackpot can happen at any point in the match, and it isn’t pumishable on block, we will consider all chip damage as one third of a full hp
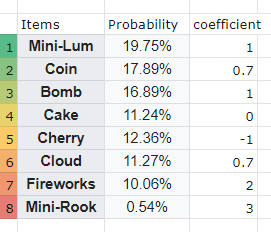
- Mini-Lum: does 1 chip damage, and pretty much guaranteed to help with dealing max damage possible
- Coin: does 1 chip, but requires a very specific range to be useful, so value decreased to 0.7
- Bomb: While it still only does 1 chip, it stuns for a long time, and hits almost all floor
- Cake: doesn’t do anything, could cost a lot in the long run, but you could get the cake too for another Jackpot, or use the cake as a bait to get more damage, so let’s leave it at zero
- Cherry: can cost from -3 chip to +3 chip, and since it can save opponent that is on 1 hp, and we want to be as modest as possible with the evaluations, so -1 would already be quite generous
- Cloud: very useful for preventing opponent from jumping in (Coin in the case doesn’t do a good job at that), but also requires very specific range to work, though it covers more vertical space, 0.7 would be okay
- Fireworks: 2 chip pretty much always guaranteed when fireworks show up, full 3 chip is very common, but not as much
- Mini-Rook: contrary to what you may think, it actually only does 1 chip damage, but if you encountered mini-Rook, you know it’s worth a lot, and also its chance is so low, it barely has any influence on average results. If we put it as 0 or 5 chip, the difference on overall damage is just 0.2 chip. I put it as 3
-
Is it fare to look into each item individually?
Not really, if we got 3 clouds and a cake, or 2 cakes and 2 coins, that would be a very bad roll, and would not guarantee 3 chip and 2 chip respectively, and just to be extremely generous to Lum, let’s say in total it’s the sum of values of each item minus 1 if it’s above zero (if it’s below zero, it means a lot of cherries got out, and it’s not necessarily that bad either). While it doesn’t account for every situation, and doesn’t exactly match what actually can happen in a situation (when Jackpot gives 4 fireworks, it usually can hit for 5-12 chip damage, and can go as low as 2 chip), it will do for some margin of approximation -
So how do we count in the end?
For each iteration my sheet generates 4 numbers between 0 and 10000, every number proportionally corresponds to the items. In the colored cells you see what item value it is, 4 numbers are generated because Jackpot generates 4 items. In the first untitled white colomn it just calculates the sum of the items’ values, first iteration gave a Cherry, 2 Lums, and a Firework, sum for their values is 3.
Next column just subtracts 1 from that if the value is positive. 3 - 1 = 2
That happens for twelve thousand iterations. After which all values are added and divided by their amount to get the average (on the picture it’s 2.104833), also the mode (3.7) and the median (1.7) is found. Standard Deviation is found in another column out of view
At first I had just one thousand iterations, which was clearly not enough, so I increased the number to 12 thousand, and got the results:
TL;DR #1
On average, being very generous to Lum’s opponent, Jackpot guarantees approximately 1.75 ± 0.05 chip damage. The most common value is the same as median 1.7 chip damage. Standard deviation is 1.40 ± 0.05 chip damage, which is a lot. It means while on average you are guaranteed to get about 2 damage, in actual game you are likely to get anything from 0 to 3 damage, but getting into negatives or above 4 is very lucky or unlucky
Here’s a graph of one of the iterations showing a kind of demonstration of the numbers I just told
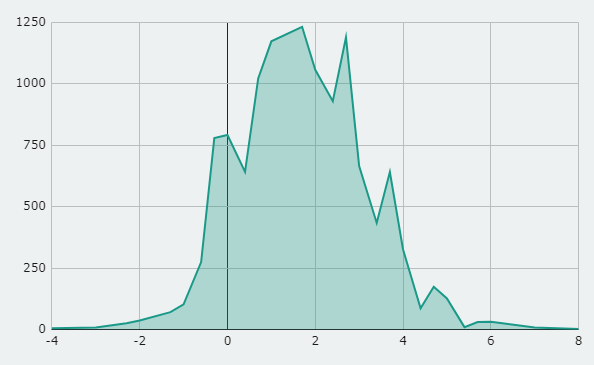
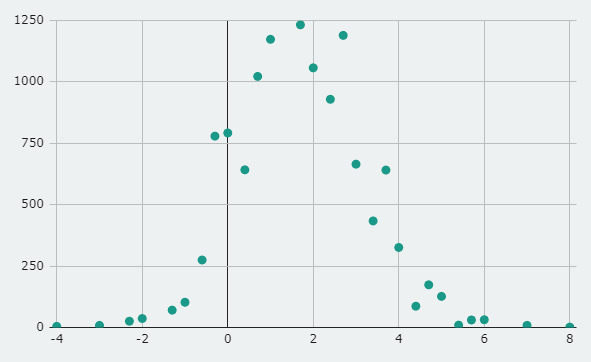
(May not look the same in your simulation)
Zero obviously has a bump since all positive numbers get 1 substracted, which makes more values for zero
Again, that was a generous, modest approach to the calculation. What if we were a little bit more confident
(also -1 only implies to the numbers between 0 and 3)
The results here are 3.26 ± 0.05 chip damage on average, 4 damage is the median and the mode number of chip damage. Standard Deviation is 2.22 ± 0.05 chips
Graphs for this case look a little bit more extreme
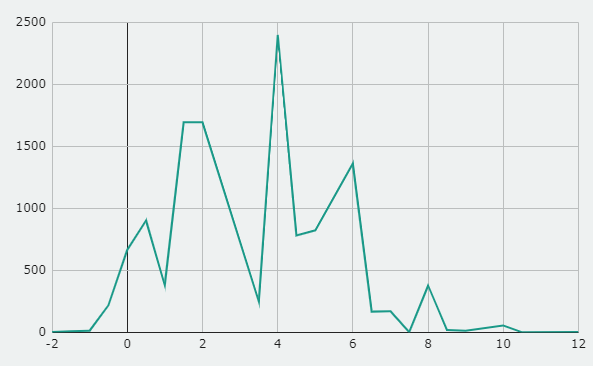
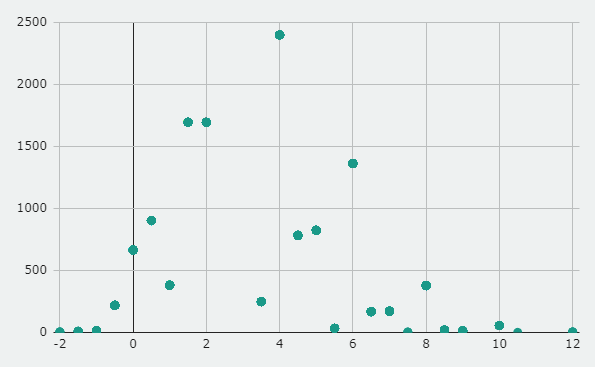
It’s because it’s not very likely to get a .5 value, with the rule of >0 and <3 it made for somesthing looking like mostly mess, but you can potentially see it’s roughly what we expect from the graph.
TL;DR #2
Whatever the actual guaranteed damage is, it should be between 1.7 and 4 with numbers outside of that range being highly unlikely. I would say on absolute average with right spacing you can get 2 chip damage almost guaranteed, 3 if you’re a little bit lucky.
Zadberry actually went to test that in-game, and got 0.83-1.19 chip damage on average out of 50 tries, so probably model needs some work
So, if you’re gonna block Lum gS at range where coins and clouds would maybe hit you, know what you’re doing. If you are Lum, learn the spacing so they don’t just jump out
Later could add an appendix on different Jackpot ranges